CARLA

Context-Adaptive Reinforcement Learning using Unsupervised Learning of Context Variables

Hamid Eghbal-zadeh*, Florian Henkel*, Gerhard Widmer
*: equal contribution.

[paper] [environment] [code]

Teaser

Introduction

In Reinforcement Learning, an agent interacts with an environment through receiving observations, executing actions, and receiving rewards. The goal of the agent is to maximise the cumulative reward that is defined based on the task at hand. In some scenarios however, the behaviour of the environment as well as the distribution of the observations can change over time. Under certain conditions, the change in the observation distribution is caused by some variability that changes the context of the environment. Therefore, a change in context affects the distribution of the environment's observations. As such changes may occur numerous times, not only does the agent have to adapt to the new contexts, but it also has to remember the previous ones. This problem is known as Contextual Reinforcement Learning (CRL).

As an example, consider a setting where users interact with a website, and the goal of the website is to adapt to the user's needs, which might change depending on the current user. However, the behaviour of the user -- the environment -- is actually affected by some unobserved parameters such as age and gender. If the goal of the agent -- the website -- is to adapt to the needs of the user, it is often helpful to be able to infer the user's characteristics and adapt to them. Another example is a robot that sees the world through a camera, where the time of the day (day/night) or the surrounding location can affect how the robot perceives its environment. Hence, it is crucial that an agent can detect a context, and be able to adapt to it.

In this paper, we provide a definition for Contextual Reinforcement Learning that assumes changing the context, affects the distribution of the states of the environment, resulting in a change in the distribution of the observations. Our definition is motivated by the generative process in a contextual world, where the context variables affect the states of the generative model of the world. Given this definition, we provide a solution using unsupervised learning of the context variable that allows for a better adaptation of the policy based on the context. More generally, in this work we are trying to answer the following questions:

Does knowing the context variable help the policy to better adapt to different contexts?
What characteristics does a predictive model need to predict context from observations?
Can our learnt context variable help the policy to better adapt to different contexts?

In order to answer these questions, we conduct a set of experiments to test the performance of an agent with and without knowing the context variable. Additionally, we conduct experiments to investigate whether disentanglement is actually helpful for estimating the context. Further, using our proposed approach, we estimate the context variable in an unsupervised manner, and compare the performance of agents with and without this estimated variable.

Problem Definition

A Partially Observable Markov Decision Process (POMDP) is defined as a tuple $(\mathcal S, \mathcal A, \mathcal P, \mathcal R, \Omega, \mathcal O)$, with $\mathcal S$ being the state space , $\mathcal A$ the action space, $\mathcal P$ the transition probabilities, and $\mathcal R$ the reward function. In this setting, the agent does not directly observe the true states of the environment, but receives observation $o \in \Omega$. This observation is generated from the underlying system state $s$ and the received action $a$, according to the probability distribution $o \sim \mathcal O(o \vert s, a)$.

In this work we consider finite-horizon episodic Contextual POMDPs (CPOMDPs). At the beginning of each episode an agent will encounter a specific POMDP depending on a randomly sampled context $c \in \mathcal C$, which we assume to not change over time within an episode. While for regular POMDPs, the goal of an RL agent is to learn a policy $ \pi(a\mid o)$ that maximizes the expected cumulative reward, in CPOMDPs the agent has to learn a policy $ \pi(a \vert o, c)$ that further depends on a context $c$.

Generative Process

We assume a generative process is in place such that everything within the environment is happening in a two-step generative process. First, a multivariate latent random variable $z$ is sampled from a distribution $P(z)$ , where $z$ corresponds to semantically meaningful factors of variation of the observations (e.g, shape, colour of the objects; density of objects). Second, the observation $x$ is sampled from a conditional distribution $P (x \vert z) $. We assume that the observation space has higher dimensionality than the semantic space, hence, the data space can be explained with substantially lower dimensional and semantically meaningful latent variable $ z$ , and is mapped to the high dimensional observation space $x$.

Generative Process in Contextual Reinforcement Learning

In Contextual Reinforcement Learning, we assume that the environment $\mathrm{E}_{z}(o_t, a_t)$ generates the next observation $o_{t+1}$, given the current observation $o_t$ and action $a_t$, i.e., $o_{t+1}=\mathrm{E}_{z}(o_t, a_t)$, with $z$ being a variable controlling its statics (e.g, shape or size of objects). In our generative view, the observations of an episode are generated from a generative model $\mathrm{E}_{z}(o_t, a_t)$ in 3 steps as follows. In the first step, a multivariate latent random variable $c \in \mathcal C$ is sampled from a distribution $P(c)$, where $c$ corresponds to a context. In the second step, a multivariate latent random variable $z$ is sampled from a conditional distribution $P(z \vert c)$, where $z$ corresponds to the state of the environment that controls the statics, defining how the environment generates the next observation, given he current observation and action during an episode. In the third step, the next observation $o_{t+1}$ is generated from the environment's generative model $\mathrm{E}_{z}(o_t, a_t)$.

Proposed Approach

In this section, we propose Context-Adaptive Reinforcement Learning Agent (CARLA), which is capable of adapting to new contexts in an environment, without any supervision or knowledge about the available contexts. CARLA consists of two parallel networks: a \textit{context network}, and a representation network. The context network aims at learning the context variable, while the representation network is aiming at learning a suitable representation from the environment. The output of these two networks are then further feed into the policy network, where an adaptive policy is formed given the environment variables and the context variable. The policy network then adapts the current policy, based on the context variable. A block-diagram of CARLA is provided below.

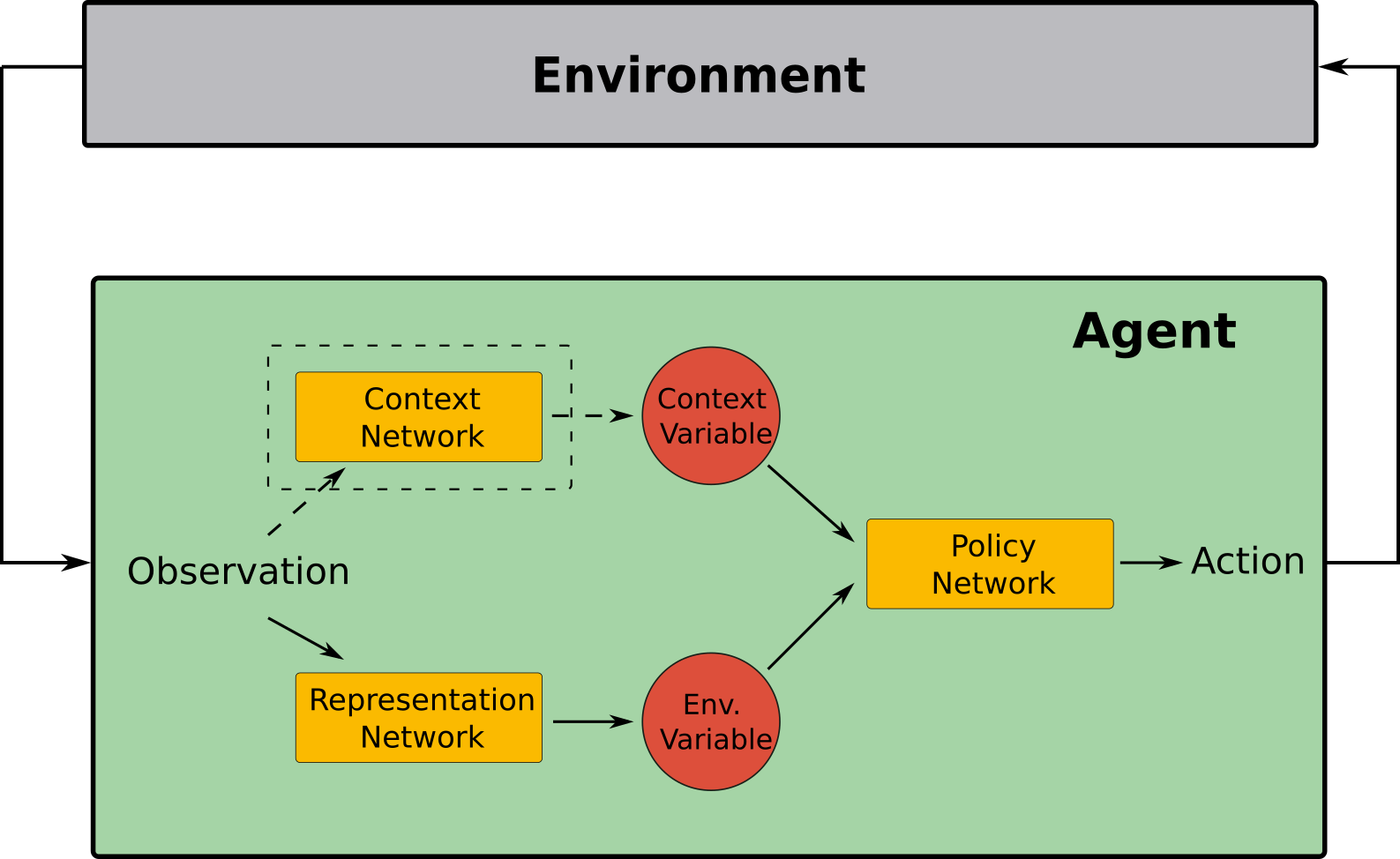
As detailed before, our assumption in the generative process is that the context variables define the statics of the environment, which in turn defines the distribution of the observations within an episode. The aim of the context network is to reverse this process and estimate the context vector given the observations. As shown in the Figure below, it contains two main modules: a feature disentanglement module and a context learning module. The context network first estimates the environment's statics, and further uses it to learn the context variable. This context factor is then feed to the policy network, in order to adapt the policy to the current context.

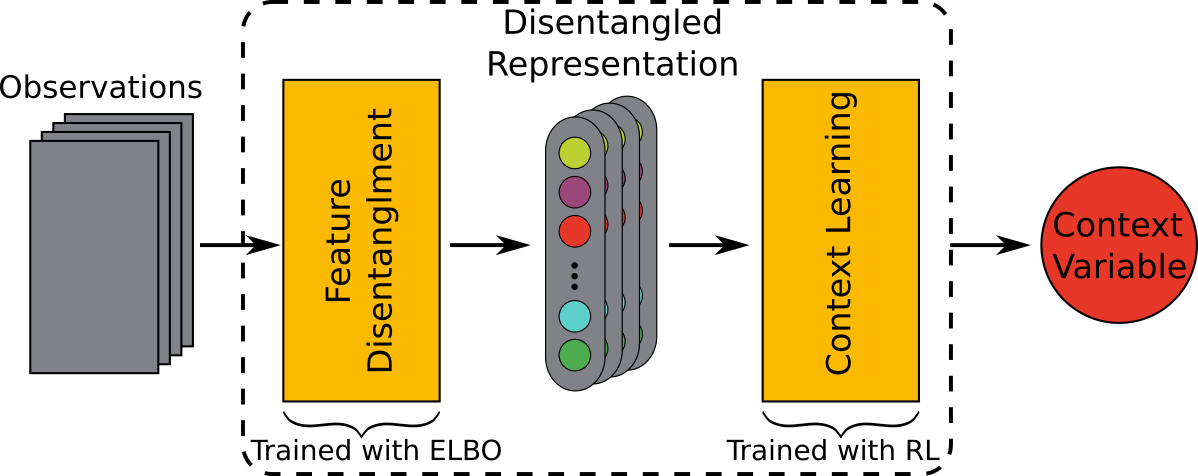
The feature disentanglement module is an encoder part of a Variational Autoencoder (VAE), which is trained with annealing the Kullback Leibler (KL) Divergence term of the Evidence Lower Bound (ELBO). The VAE is trained using random samples drawn from an experience replay buffer. The context learning module is trained online given the observations received in each episode, along with the representation network and the policy network by optimizing the RL objective. This module learns upon the disentangled states of the environment, extracted using the feature disentanglement module explained above.

The graphical models for various approaches in CRL is provided in the Figure below.

As can be seen, our model has a different graphical model than DARLA (Higgins et. al, 2017) and VALOR (Achiam et, al. 2018). The main idea in CARLA, is to learn disentangled factors from the environment using pre-selected training data, in a similar manner to DARLA. In contrast, CARLA uses a recurrent context network that can build the sequential relationship for the disentangled factors, to predict the context variable, which might be useful in a partially-observable setting to infer the dynamics. Further, CARLA allows the agent to learn an unconstrained representation from the environment during training the agent via interacting with the environment. Although VALOR uses a sequential decoder, it differs from CARLA in various ways. For example VALOR assumes an observed context, in contrast to CARLA which estimates the context variable using a sequence of disentangled factors.

Citation

@InProceedings{pmlr-v148-eghbal-zadeh21a,
     title = {Context-Adaptive Reinforcement Learning using Unsupervised Learning of Context Variables},
    author = {Eghbal-zadeh, Hamid and Henkel, Florian and Widmer, Gerhard},
    booktitle = {NeurIPS 2020 Workshop on Pre-registration in Machine Learning},
    pages = {236--254},
    year = {2021},
    editor = {Bertinetto, Luca and Henriques, João F. and Albanie, Samuel and Paganini, Michela and Varol, Gül},
    volume = {148},
    series = {Proceedings of Machine Learning Research},
    month = {11 Dec},
    publisher = {PMLR},
    pdf = {http://proceedings.mlr.press/v148/eghbal-zadeh21a/eghbal-zadeh21a.pdf},
    url = {http://proceedings.mlr.press/v148/eghbal-zadeh21a.html}
}